(Meant for my Intro to Homological Algebra Summer Seminar Group at SJC)
Last time we met we discussed groups, where we can recall that
A group,
, is a set with a binary operation
which is associative, has an identity, and has inverse elements.
Example: 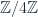
We’re going to next consider how to take a group, and a subgroup,
and form the quotient group
. As an example, let’s use the group
of integers under addition. Consider the subgroup
, which contains elements like 12, 4, -100, etc, but not 3, 2, -99, etc. We will now define an equivalence relation on
by saying that the elements
and
are equivalent, which we will denote by
, if
.
Let’s go through some examples of elements which are equivalent:
and so
. [Edited 6/13]
and so
.
and so
.
If we went through all possible combinations, we would see that there are exactly 4 equivalence classes of elements that we are partitioning into:
Just to absolutely clear, for each of these sets, if I take two elements in the same set, and I look at their difference, it will be a multiple of 4; if I take two elements each from different sets, their difference will not be a multiple of 4.
Here’s where things get trippy: we will now take the infinitely-large set, , and just treat it as four elements:
,
,
, and
. Note: a shortcut for knowing which set is which is by looking at the remainders of the elements, so 5 is in
because when I divide it by 4, the remainder is 1. And -3 is in the [1] as well because when I consider: (-3) – (5)= – 8, I get an element in
!
So now let’s add elements in our set, . Remember that each
is a subset of integers. Suppose I took the number
and added it to the element
. Well 2+3 = 5, but there is no element “
“, is there? Well if there was, what would it be? The set
would be the set of integers which are equivalent to the number 5, under the rule “~” we used above. Well note that
, and so it turns out that
(by the properties of an equivalence relation, which we will have to go through carefully and formally). The point is…
!!
Example: 
Let us do the same thing as we did above to partition the integers, except now if
. Note that we now have 5 elements in our set, which the rest of the world refers to as
. Note that I chose to use
in place of
; there is a reason which you might come to realize but it isn’t super important.
While the integers only form a group under addition, you should explore this new set and see if it forms a group under addition or multiplication or both!? Either way the answer should be surprising and interesting.
Example: 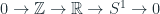
Finally, I would like to introduce a more geometric example. The previous examples ended up with a finite number of elements in our quotient, and everything was down to arithmetic. Consider again our lovely set of integers, , which are a group under addition. But now consider the subgroup
of integer-spaced multiples of
, each of which is a real number (whatever that means, amiright?). Anyway, I’m now going to consider the group
, but what the heck is this group?
Well I chose because that is the circumference of the unit circle. So notice I have a function
by sending
which takes each real number and maps it on the unit circle. Which real numbers go to zero? The multiples of
! Which real numbers get sent to
? The real numbers
where
is any integer!
So we’ve taken the real line, and thought of any two numbers which are -apart as being glued together, and if you try to draw this picture you should see a circle!

Well this picture isn’t really what I want you to see but I’m tired and it should be good enough to get your creative brain going!
Food For Thought: Preparing for our next meeting
After having slowly read through this blog post, which could take hours, I encourage you to try and go back through our notes to see if any of the examples, propositions, exercises, etc, make any more sense than they did. Specifically, I want us to finish up this discussion on quotients in our next meeting and then continue on to some other ideas, which I will now appropriately tease…
Note that we started with the additive group of integers, and when modding out by , we actually get some nice multiplicative structure. What if a group had both an additive and a multiplicative structure, do quotients make sense for playing nicely with both of these structures simultaneously? The answer to this leads us to a study of rings (groups which also have some multiplicative structure; not necessarily inverses), and modules (groups which can be multiplied by external elements; like vectors can be multiplied by numbers).
Finally, in the last example I gave, the title for that example had some arrows connecting the integers, to the real numbers, and then to the circle, . Those arrows are actually functions which allow the group structures of each group to communicate with each other. This type of function is called a homomorphism and will be central to our study of Homological Algebra.

Thanks for the content, but I think you have a typo! Where you specify examples of which two elements are equivalent, your third example shows that 4 is clearly not equivalent to 5, but your first example shows that 4 is equivalent to 5…! I noticed it as soon as I realized that 5 is clearly not a multiple of 4, so maybe you meant to say that 4 ~ 4.
LikeLike
Thanks, Josh! I’m fixing this now!
LikeLike